[最も人気のある!] 中心角 公式 265901-三角锥 中心角 公式
次に、中心角について解説していきます。 中心角を一言で言うと、円周角の中心バージョンです。 円周角では、点を円周上に3つ置きましたが、円周上に2つ置いた点と、円の中心をそれぞれ結んだときに出来た角を中心角といいます。 これを図にすると、 このようになります。 中心角も円周角と同じように、弧によって角度は変わります。 また、1つの円において、等しい弧であれば、中心角も等しおうぎ形の弧の長さ、面積、中心角の求め方と公式 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は180°、さらに半分切りとれば中心角は90°になります。 ケーキを半分に切ったり、三分の一にしたりするときを想像するとわかりやすいでしょう。 おうぎ形の弧の長さと面積は下のプリントのように求めます。 半径をr、中心角をa°とします。 弧の長さ 面積 重要なポイントは下の 円すいの展開図、中心角の公式を知って5秒で解こう♪ 面積 面積 円すいの展開図の中心角を求めなさい。 円周率は314とします。 知りたがり 何に注目 すれ

如何求弧长 10 步骤 包含图片
三角锥 中心角 公式
三角锥 中心角 公式- 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だよ だから、きっちり 本質 を理解しようね圆的计算公式: 1圆的边长即的周长C=2πr=或C=πd 2圆的面积S=πr2 3扇形弧长L=圆心角(弧度制)r = n°πr/180°(n为圆心角) 4扇形面积S=nπ r 2 /360=Lr/2(L为扇形的弧长) 5圆的直径 d=2r




扇形中心角公式 ニスヌーピー壁紙
中心角を \(x\) とすると、扇形の面積公式を利用し $$\pi \times 6^2\times \frac{x}{360}=12\pi$$ という方程式を作ることができます。3 两角和与差的余弦公式的五种推导方法之对比 .人民教育出版社 引用日期 4つまり, 「中心角 θ rad 」というのと「中心角 θ 」というのは,同じことを意味します. 例1 半径1,中心角が π 3 の扇形は下図のようになります. 半径1の円においては,「 (中心角)= (弧の長さ)」なので弧の長さ ℓ は ℓ = π 3 です. 例2 半径2,中心角が π 3 の扇形は下図のようになります. 例1のように, 半径1の円においては「 (中心角)= (弧の長さ)」したが,半径が2になれば弧の長さも2倍に
6 直齿径节齿轮 7 斜齿径节齿轮 11、齿底直径 14、齿底圆直径 15、齿顶圆直径 移位螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②) 5、压力角(齿 「扇形の中心角の求め方」の公式ってチョー便利。 教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、x = 180L/πrになるってやつさ。 つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。 たとえば、半径 4 、弧の長さが 6π の扇形があったとしよう。 この「扇形の中心角」を求めたいとおうぎ形の公式 弧の長さ = 円周 × 中心角 360° 中 心 角 360 ° = 直径×314 × 中心角 360° 中 心 角 360 ° おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時に
圆心角是指在中心为O的圆中,过弧AB两端的半径构成的∠AOB, 称为弧AB所对的圆心角。 圆心角等于同一弧所对的圆周角的二倍。 圆心角的计算公式 ①L (弧长)= (r/180)Xπ(n为圆心角度数,以来下同); ②S (扇形面积) = (n/360)Xπr2; ③扇形圆心角n=(180L)/(πr)(度)。 ④K=2Rsin (n/2) K=弦长;n=弦所对的圆心角,以度计。 扩展资料 圆心角的性质源 ①顶点是圆心; ②两条边都与圆周相交工具齿形 螺旋齿 蜗轮、蜗杆的计算公式: 1,传动比=蜗轮齿数÷蜗杆头数 2,中心距=(蜗轮节径蜗杆节径)÷2 3,蜗轮吼径=(齿数2)×模数 4,蜗轮节径=模数×齿数 5,蜗杆节径=蜗杆外径2×模数 6,蜗杆导程=π×模数×头数 7,螺旋角(导程角)tgB=(模数×换位置的公式很容易,这个公式是将左和前的棱相互交换 rur#39;u r u#39;




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=nπR÷180。 例:半径为1cm,45°的圆心角所对的弧长为 l=nπR÷180 =45×派×1÷180 约等于0785 (cm) 如果已知他的沿圆锥体的一条母线和侧面与下底面圆的交线将圆锥体剪开铺平,就得到圆锥的平面展开图。 它是由一个半径为圆锥体的母线长,弧长等于圆锥体底面圆的周长的扇形和一个圆组成 円周角と中心角 定義 点 O O を中心とする円 O O の ⌢ AB A B ⌢ と, ⌢ AB A B ⌢ を除いた円周上の点 P P に対して, ⌢ AB A B ⌢ に対する 円周角 : ∠APB ∠ A P B ⌢ AB A B ⌢ に対する 中心角 : ∠AOB ∠ A O B スポンサーリンク演習問題で理解を深める! (1)半径6㎝、中心角1°のおうぎ形の弧の長さと面積を求めなさい。 (1)解説&答えはこちら 答え 弧の長さ: 面積: 弧の長さを求めるためには の公式にあてはめます。 円の面積を求めるためには の公式にあてはめます



万能公式 快懂百科




图形和几何体公式 1 Ai猪的博客
扇形の中心角の求め方3パターン を見てみてね ちなみに、 中心角を求める公式 もあって 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線 こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど! 何を求めるのも公式だよりってなると "応用問題に対応できない" , "覚える数が多すぎて忘れちゃう" ってことになるから、公式最強~な勉強はやめる方がい中心角の割合 72/360 = 1/5 円の面積 π × 5 = 100π 円の面積は半径×半径×円周率なので、 半径を求めるには 面積÷円周率 で求められる 100π ÷ π = 10 cm 弧の長さと中心角から半径を求める場合も同様に、中心角の割合から円周を算出して、円周を求める逆の計算をおこないます。 中心角72度、弧の長さ4πcmのおうぎ形の半径は? 中心角の割合 72/360 = 1/5 円の円周 4π × 5 = π 円の円周は直圆心角是指在中心为O的圆中,过弧AB两端的 半径 构成的∠AOB, 称为弧AB所对的圆心角。 圆心角等于同一 弧 所对的 圆周角 的二倍。 1 圆心角的度数等于它所对的弧的度数。 在同圆或等圆中,若两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等




備戰19年中考初中數學滿分突破錦囊之和圓有關的計算 Itw01




如何求弧长 10 步骤 包含图片
おうぎ形の弧の長さ = 直径 × 円周率 × 中心角 ÷ 360 $$扇形の弧の長さ=直径 \times 円周率\times \frac{中心角}{360}$$ 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 二倍角公式 5 万能公式(可以理解为二倍角公式的另一种形式) 万能公式告诉我们,单角的三角函数都可以用半角的正切来表示。 6 和差化积公式 7 了解和差化积公式的推导,有助于我们理解并掌握好公式: 8 つまり、 扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができる んだ。 たとえば、 半径 4 cm、弧の長さが 6π cmの扇形があったとしよう。 この「扇形の中心角」を求めたいときは公式をつかえば一発。 3秒ぐらいで中心角が求められるよ^^ 中心角の公式は、 x = 180L/πr だったよね? これに半径r=4cm、弧の長さL= 6πを代入してやると、 x = 270° っていう答




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
半径3cmで面積が3π㎠のおうぎ形の中心角を求めます。 まずは同じ半径 (3㎝)を持つ円の面積を求めます。 3×3×π=9π あとは公式に当てはめていくと 式が完成します。 あとは約分してやって、計算あるのみ! これで中心角が1°だと求めることができ→1コマあたりの中心角は 360°÷8 = 45° xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135° 2 135 ° 2 = 675° 同様に、yは2コマ分の中心角の半分 → y = 1 2 1 2 (2×45°) = 90° 2 90 ° 2 = 45° 同じ弧より 円周角も等しいので 図のような場所もy ∴ zは外角より (スリッパより) z = xy = = 1125° 《 例 》 図のようなとき、AB:CD を求めましょう 図のようにx, y (同じ弧に対す 扇形が完全な円(中心角360°)に対してどれくらいの割合の大きさになっているのかを、中心角 a a を用いて a 360 a 360 で表しています。 完全な円の場合円周は 2πr 2 π r なので、弧の長さはこれに a 360 a 360 をかけた値になります。 『直径×314× 中心角 360 × 314 × 中 心 角 360 』⇒『2πr× a 360 2 π r × a 360 』 ちなみに、扇形の弧の長さについても考え方は詳しく解説して




扇形弧長公式扇形弧長公式1 Qqkaii



对有源带通滤波器的一些认识 Eda365电子论坛通信数码 人工智能 计算机 半导体 手机家电消费电子硬件门户网站
三维GIS显示中,利用太阳高度角和方位角计算光照 利用太阳方位角和太阳高度角进行光照计算的时候,需要注意: – 1、 坐标系是球坐标系,具体正方向如下图所示: 极坐标公式: x=rsinθcosφy=rsinθsinφ z=rcosθ φ:由x轴出发,逆时针旋转到地物方位所得的角度; θ:由z轴出 円周角が ∠ A P B = 中心角が ∠ A O B = 2 × となり、「円周角が中心角の半分である」ことを示せました。 どのパターンでも「円周角が常に中心角の半分である」ことから、「同じ弧 A B に対する円周角は等しい」ことも分かります。 円周角の定理とは弧长计算公式为: (Central Angle / 180°) •π • r 黄色区域为扇形 扇形面积公式为: (Angle AOB / 360°) •π • r² 绿色面积为拱高面积 此面积大小=扇形面积- AOB三角形 推荐 九九参考计算器 支持我们使用 京东360buy 当当 购物支持我们。




弓形面积计算器 搜狗百科



扇形中心角 高中数学综合论坛 中学生答疑交流论坛 上海腾飞教育学习论坛




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




扇形的面积计算公式扇形的面积公式是什么如何计算扇形的面积



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ



沪教版初中数学pdf初中数学几何重难点 中考失分较多 圆模块方法攻略 小初高题库试卷课件教案网




如何求弧长 10 步骤 包含图片




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



中心角 玄数



球的中心角的度量是多少 教育小本子




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



倍角公式 图片欣赏中心 急不急图文 Jpjww Com



棱柱的侧面积公式直棱柱的侧面积 全面积怎么求 麦税尼网




如何求弧长 10 步骤 包含图片




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




中1 中1 数学 範囲 おうぎ形の中心角の求め方 大放出ぅ 中学生 Clearnote




正多边形公式 搜狗搜索




平面図形 おうぎ形の中心角 中学数学 定期テスト対策サイト



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻



三角函数公式 快懂百科



1




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
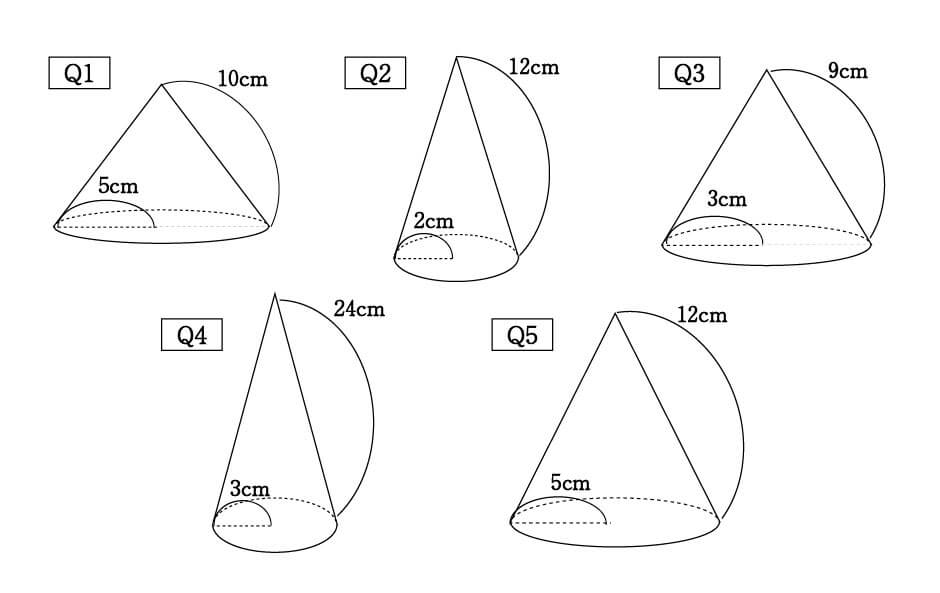



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



圆锥面积公式图解 第1页 要无忧健康图库




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形中心角公式 ニスヌーピー壁紙




二阶有源带通滤波器滤波原理 Xiao Yao Ke的博客 Csdn博客 有源带通滤波器
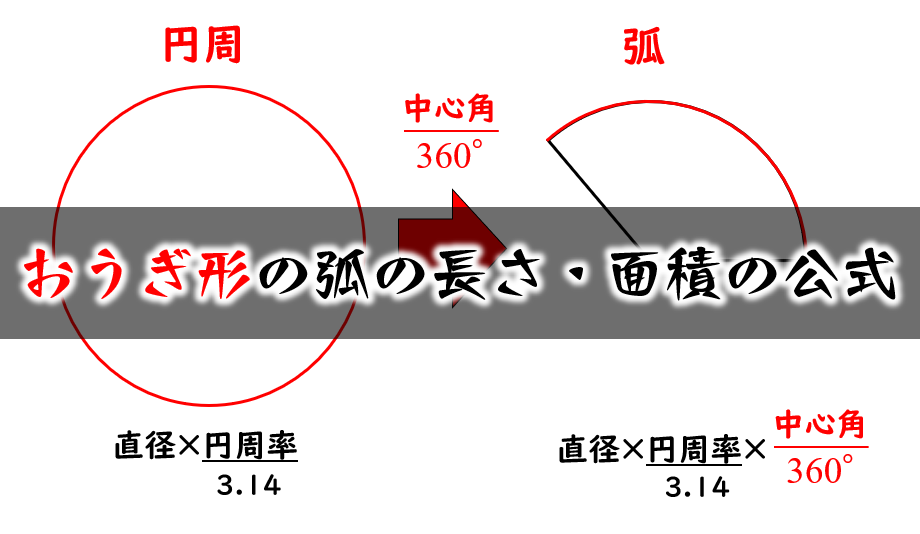



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




扇形面積計算計算弧長及扇形的面積 Ttvu



1



初中数学圆相关知识点汇总 建议收藏 切线




扇形面積弧度中學數學漫談一一扇 Hrkpar
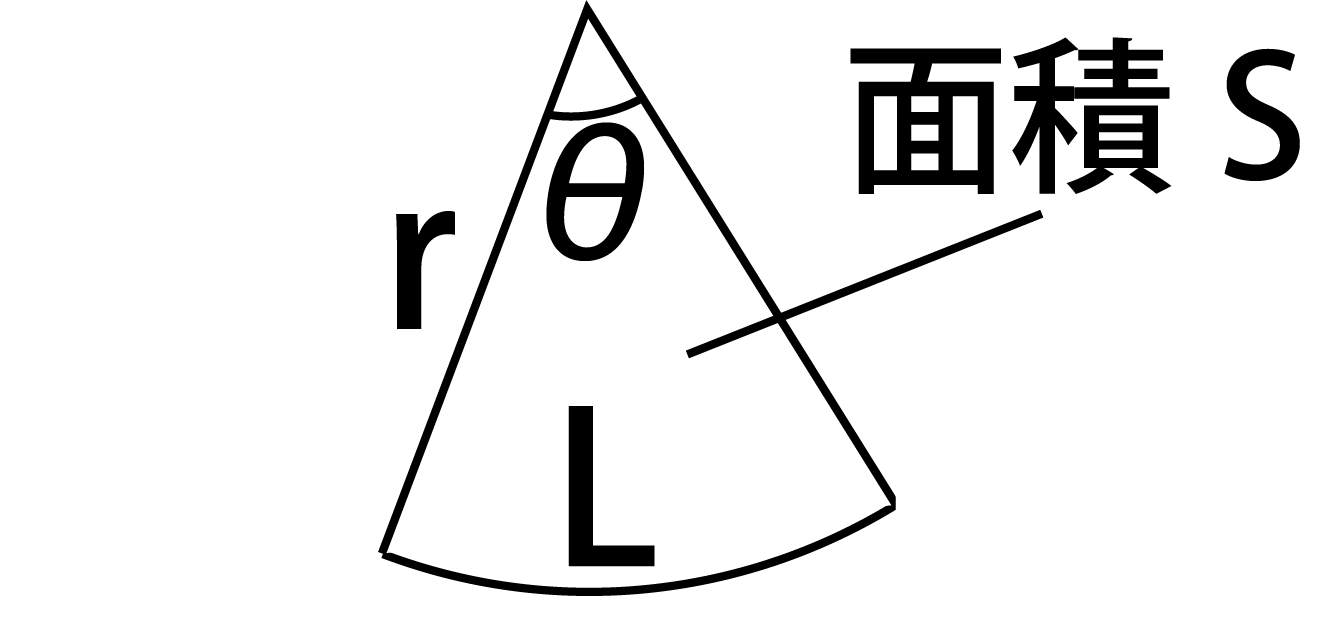



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



高一数学三角函数诱导公式检测试题



东丽中学欢迎您




上中心角公式 シモネタ




扇形面積公式弧長14 Zilhc




中1数学のおうぎ形の公式が覚えられません そろそろテストなのでやばいんです Clearnote




扇形の中心角の求め方を教えてください Clearnote



记三角函数公式 这篇文章教你记得又快又准



1




三節等徑圓管90 彎頭展開計算 每日頭條




如何计算圆的面积 提示 November 21




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
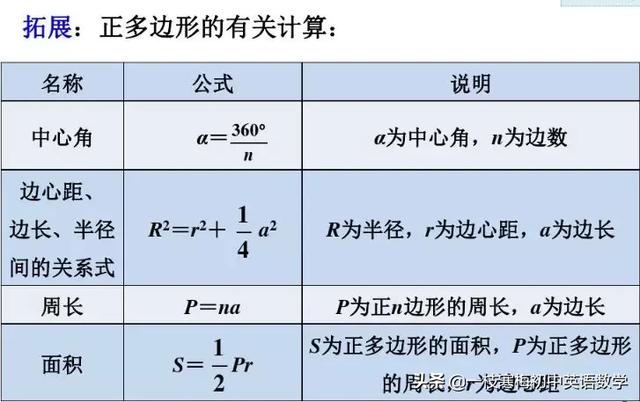



一个点到多边形顶点距离相同 北师大版丨九下数学3 8 圆内接正多边形知识点精讲 Weixin 的博客 Csdn博客




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



おうぎ形の中心角の求め方 Youtube



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋
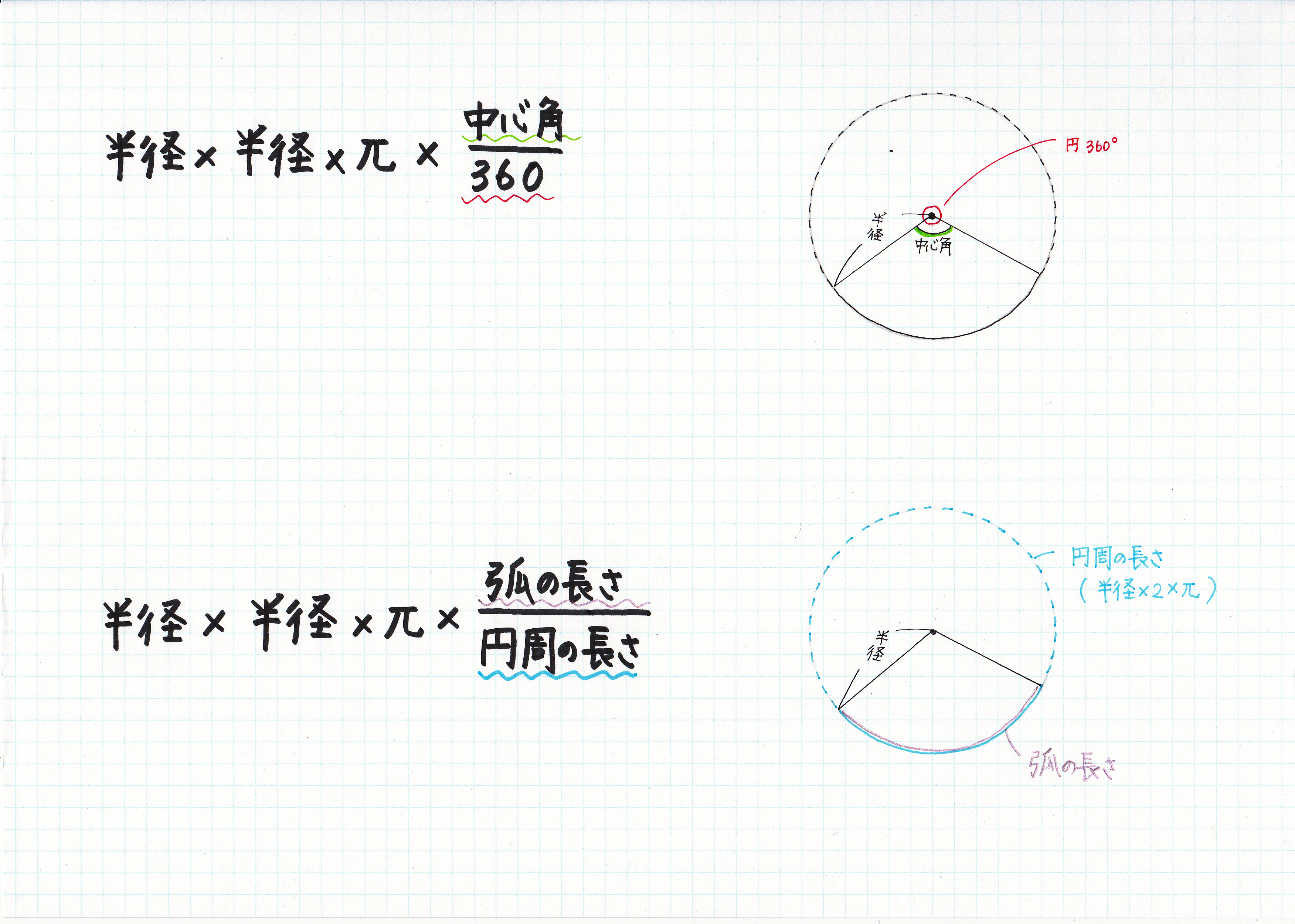



おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ



Arc Area Formula




如何求弧长 10 步骤 包含图片



网络画板 数学教育之窗




扇形 中心角 公式 学び 教科書 勉強



年中考数学总复习第22讲与圆有关的计算新版新人教版 淘文库




中1 数学 空間図形9 おうぎ形の公式 17分 Youtube




類題15求解 扇形半徑為30 中心角60度 則內切圓半徑為何 Clearnote




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




高中数学三角函数基础知识下载 Ppt模板 爱问共享资料



多路负反馈二阶带通滤波电路及其multisim仿真验证




内接角公式 数学和多媒体 必威app下载




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




计算圆扇形的面积 提示 21




Study 円錐の側面 扇形 の中心角の求め方 中2数学 ちくらっぽインク



非非标链轮之日本标准jis B1802 19链轮 任丘市华鹏链条链轮有限公司
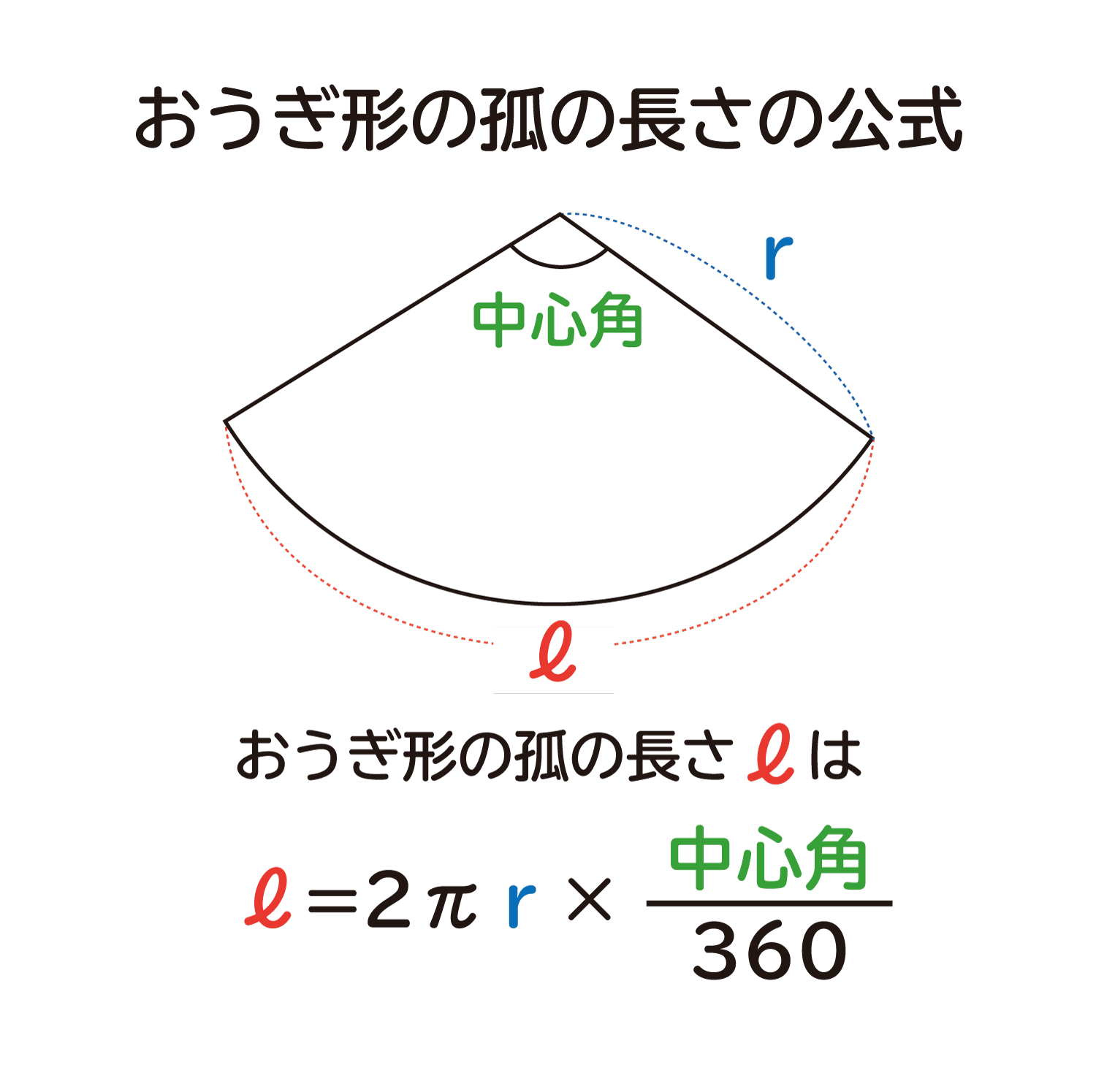



なぜ おうぎ形の孤の長さは2pr 中心角 360 なのか を説明します おかわりドリル




扇形の面積の求め方 公式と計算例




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形面積證明中學數學漫談一一扇 Vscizr




数控车椭圆宏程序编程解析下载 Word模板 爱问共享资料




円 扇形 の面積 周や弧の長さの公式 数学fun




怎么寻找弧线长度 最有妙招网




如何求弧长 10 步骤 包含图片




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




数控车椭圆宏程序编程 很难吗 这样学习十分轻松 资讯咖




怎么计算圆的半径 最有妙招网
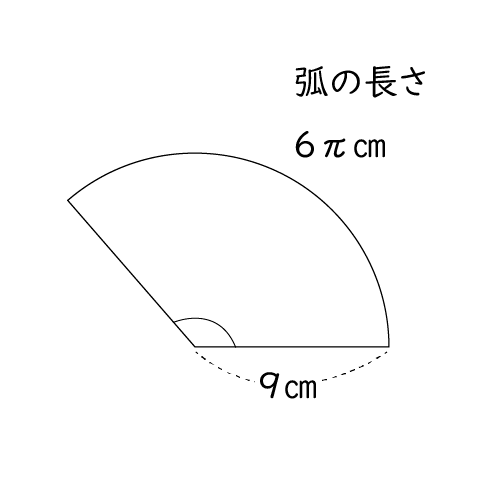



中学1年生数学 おうぎ型の中心角の求め方 長野地区 Itto個別指導学院 長野市の学習塾




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




如何求弧长 10 步骤 包含图片



中心角计算公式 扒拉扒拉
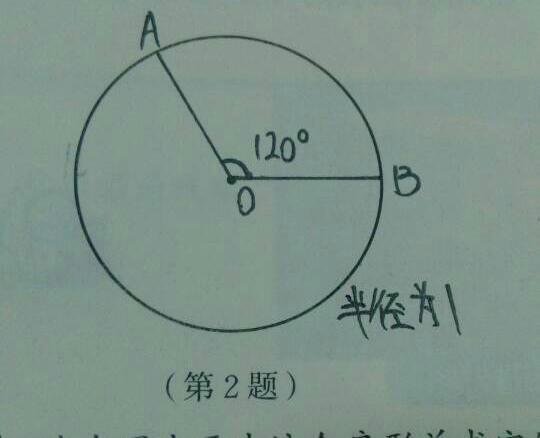



圓心角 定理 計算公式 性質 中文百科全書
コメント
コメントを投稿